Think you’ve got your head wrapped around Circles? Put your knowledge to
the test. Good luck — the Stickman is counting on you!
Q. Given one line and one circle that you can arrange in any way you like, what is the minimum number of points where they intersect?
0
1
2
3
4
Q. Given one line and one circle that you can arrange in any way you like, what is the maximum number of points where they intersect?
0
1
2
3
4
Q. Suppose line q is tangent to ⊙O at the point P. Which of the following must be true?
Line q is parallel to OP and is not parallel to any other radius of ⊙O.
Line q is perpendicular to OP and is not perpendicular to any other radius of ⊙O.
Line q is parallel to OP and may be parallel to another radius of ⊙O.
Line q is perpendicular to OP and may be perpendicular to another radius of ⊙O.
None of the above
Q. In the figure below, segments AC and BC are tangent to ⊙O at points A and B, respectively. If AO = 3 cm and AC = 5 cm, what is CB?
3 cm
5 cm
6 cm
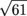cm There is not enough information to find CB
Q. What is the equation of a circle with radius 12 units and center at (3, -2)?
(x – 3)2 + (y + 2)2 = 12
(x + 3)2 + (y – 2)2 = 12
(x + 3)2 – (y – 2)2 = 12
(x – 3)2 + (y + 2)2 = 144
(x + 3)2 + (y – 2)2 = 144
Q. What is the center of the circle with equation (x – 5)2 + (y + 18)2 = 67?
(5, -18)
(5, 18)
(-5, -18)
(-5, 18)
No such circle exists
Q. What is the radius of the circle with equation (x – 8)2 + (y + 1)2 = 54?
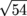units 54 units
542 units
8 units
No such circle exists
Q. What is the exact circumference of the circle with equation (x + 5)2 + (y + 2)2 = 36?
4π units
10π units
12π units
14π units
There is not enough information
Q. If line m is tangent to ⊙O at P and the slope of the line containing OP is 
, what is the slope of line m?
, what is the slope of line m? 
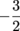
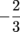
0
Q. Consider the circle with radius 6 units, centered at the origin. Where is the point (-3, 4) in relation to the circle?
In the interior of the circle
In the exterior of the circle
On the circle
Tangent to the circle
Perpendicular to the circle