Think you’ve got your head wrapped around Computing Derivatives? Put your knowledge to
the test. Good luck — the Stickman is counting on you!
Q. Let f(x) = e. Then
f ' (x) is undefined because f has no slope.
f ' (x) = 0
f ' (x) = 1
f ' (x) = e
Q. What is the derivative of f(x) = 5x + 6?
f ' (x) = 0
f ' (x) = 1
f ' (x) = 5
f ' (x) = 6
Q. Which of the following is not a power function?
f(x) = x-2
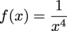
f(x) = x(0.5)
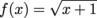
Q. For which function f(x) is f ' (x) = -3x-4?
f(x) = x-2
f(x) = x-3
f(x) = x-4
f(x) = x-5
Q. What is the derivative of f(x) = ex?
f ' (x) = ex
f ' (x) = ex(ln x)
f ' (x) = xe(x – 1)
f ' (x) = 1
Q. The slope of the function f(x) = ex is
sometimes positive, sometimes negative, and sometimes 0.
always either 0 or positive.
always positive.
sometimes positive and sometimes undefined.
Q. Let f(x) = 6x. Then
f ' (x) = 6x
f ' (x) = 6x(ln 6)
f ' (x) = 6x ln 6
f ' (x) = (ln 6)x
Q. Which function f(x) has the derivative f ' (x) = x-1?
f(x) = x-2
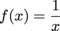
f(x) = ln x
f(x) = log x
Q. Let f(x) = cos(x). Then
f ' (x) = sin(x)
f ' (x) = cos(x)
f ' (x) = -sin(x)
f ' (x) = -cos(x)
Q. Which function's derivative is f ' (x) = sin(x)?
f(x) = sin(x)
f(x) = cos(x)
f(x) = -sin(x)
f(x) = -cos(x)