Cyclic Quadrilaterals at a Glance

All our lives, we've been taught that boxes are bad. We shouldn't put things in boxes (at least, according to Rosencrantz and Guildenstern). It's better to think outside the box. And it's not exactly a compliment when your grandma tells you that your figure's getting "boxy."

So if we can't put things in boxes, let's try putting them in circles.

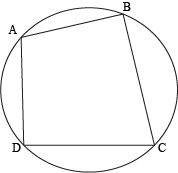
A cyclic quadrilateral is a quadrilateral whose vertices all lie on a circle. It doesn't matter if the angles or sides are parallel or congruent or none of the above. If we can draw a circle that connects all the vertices of that quadrilateral, it's cyclic. No questions asked.

Sample Problem

Which of the following quadrilaterals are cyclic?

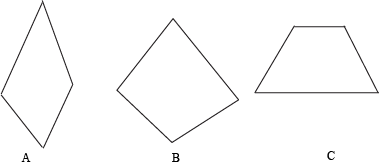
The easiest way to figure out which quadrilaterals are cyclic is to simply draw the smallest possible circle around them.

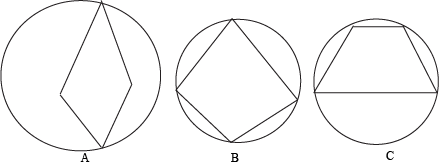
When we draw the smallest circles that we can around each quadrilateral, we see that (B) and (C) have all of their vertices on the circle. The quadrilateral in (A) has only two vertices on its circle. So (B) and (C) are cyclic, and (A) is not. Simple as that.

Well, what's so special about cyclic quadrilaterals anyway? We could stick quadrilaterals into circles all day long, but what's the point?

Opposite angles of cyclic quadrilaterals are always supplementary. That means if we can draw a circle around a quadrilateral that connects all of its vertices, then we know right away that the opposite angles have measures that add up to 180°. How's that for a point? And we're just getting started.

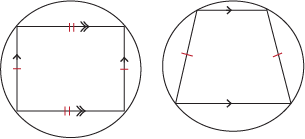
It's also true that if two opposite sides of a cyclic quadrilateral are congruent, then the other two sides are parallel. We might not have expected this, but it's true nonetheless. Just like we might not have expected Napoleon Bonaparte to have had ailurophobia (a fear of cats). But he did.

Let's say a quadrilateral is cyclic. If it has a pair congruent and parallel opposite sides, then it has to be a rectangle. If it has pair of congruent and non-parallel sides, it has to be an isosceles trapezoid.

Sample Problem

Quadrilateral PQRS is cyclic. What is the measure of ∠PSR?

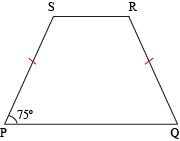
We can see from the figure that PS ≅ QR. Because opposite sides of this cyclic quadrilateral are congruent, we know that the other two sides (namely, PQ and SR) are parallel. We also know that ∠QPS and ∠PSR are supplementary because consecutive angles that share the same leg in a trapezoid are supplementary. As such, we can set up the following equation:

m∠QPS + m∠PSR = 180°
75° + m∠PSR = 180°
m∠PSR = 180° – 75°
m∠PSR = 105°

Game, set, and match.

What if we're asked to determine whether a given quadrilateral is cyclic? What do we do then? We could put our heads between our knees and kiss our bums goodbye, but we'd rather not. Instead, we've got two options:

1. Prove that all of the vertices of the quadrilateral lie on a circle. (They call this the "compass method" because we'll probably need a compass.)
2. Prove that any two opposite angles are supplementary.

Sample Problem

Is a square a cyclic quadrilateral?

All of the internal angles of a square are 90°. Opposite pairs will total 180° in measure, which means they're supplementary. Since we've proven that opposite angles are supplementary, we know that squares are cyclic. You could try this with a compass too, but we recommend drawing it on paper rather than your computer screen. Just a suggestion.