We've been focused on triangles and quadrilaterals for a long, long time. But in this geometric jungle, there exist many more shapes than just three- and four-sided animals. There are figures with five, six, seven, and even forty-two sides. And it won't do us any good to keep our heads underground like ostriches, pretending they don't exist.
If you hadn't figured it out yet, polygons are closed two-dimensional figures made up of straight line segments only. So triangles and quadrilaterals are examples of polygons, but angles, curves, and circles need not apply.
As far as naming polygons goes, we usually name them with Greek prefixes (like "tri-" and "octo-") that match the number of sides they have. Of course, after a certain point, it gets exhausting. That's why after 12 sides, we just stick to calling them 13-gons and 28-gons and 146-gons. It's easier to memorize and easier to write. Sounds good to us.
| Sides | Name of Polygon |
| 3 | triangle |
| 4 | quadrilateral |
| 5 | pentagon |
| 6 | hexagon |
| 7 | heptagon |
| 8 | octagon |
| 9 | nonagon |
| 10 | decagon |
| 11 | undecagon |
| 12 | dodecagon |
| n | n-gon |
Just like quadrilaterals, these different types of polygons also have diagonals. (Except triangles, no matter how hard they tri.) But how many diagonals will these polygons have, exactly?
Let's start by drawing non-intersecting diagonals. Quadrilaterals can only have 1 such diagonal. Drawing in the other one would intersect the first one, and they're called "non-intersecting" for a reason.
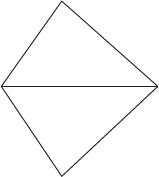
If we take a pentagon, we can draw 2 diagonals that don't intersect. The key is to draw just enough to separate the polygon into all into triangles.
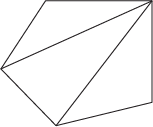
When we look at hexagons, we can break them down into 4 distinct triangles using any 3 non-intersecting diagonals.
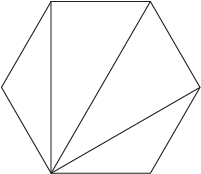
When we go to heptagons, we can have 4 non-intersecting diagonals. This could be some strange, mathematical voodoo...or it could be a special relationship between polygons and triangles? Basically, it boils down to the fact that a convex polygon with n sides can be divided into n – 2 distinct triangles by n – 3 non-intersecting diagonals.
If we go back to our smorgasbord of polygons, we know that a triangle has internal angles that sum to 180°. A quadrilateral has internal angles summing to 360°. As it turns out, pentagons have 540° worth of internal angles and hexagons have 720° worth of internal angles.
More mathematical voodoo? Not so much. A polygon with n sides has internal angles that sum to (n – 2) × 180°.
Sample Problem
Using triangles, determine the total measure of the internal angles of a quadrilateral.
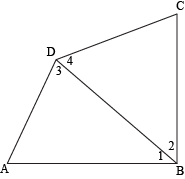
Let's draw one diagonal connecting B and D across quadrilateral ABCD. We get two triangles: ΔABD and ΔBCD. The measure of internal ∠ABC is just the sum of the measures of ∠1 and ∠2. The measure of ∠ADC is the sum of measures of ∠3 and ∠4. Meanwhile, ∠BAD and ∠BCD are shared between triangles and the quadrilateral.
When we add the angles of both triangles together, 180° + 180° = 360°. This confirms exactly what we already knew. Way to go, us.
If we did the same for a pentagon, we'd break the pentagon into three triangles, each of which contributes 180° to the sum of the interior angles of the pentagon. Adding each of these contributions gives us 540°. This also goes along with our formula, since (n – 2) × 180° when n = 5 is (5 – 2) × 180° = 3 × 180° = 540°.
Until now, we've stuck with triangles and quadrilaterals. Now that we're expanding our geometric taste, we should expand our vocabulary to match.
A regular polygon is one whose sides are equal and angles are equal. So a regular triangle is the all-too-familiar equilateral triangle. A regular quadrilateral is better known to us as a square. That's because the only quadrilateral that is both equilateral and equiangular is the square.
We can count sides, we can count angles, and we can count diagonals. (You know who loves to count? The Count.)
The number of non-intersecting diagonals, we already know, is equal to n – 3 where n is the number of sides of the polygon. But what about the total number of diagonals even when they do intersect? Well, every vertex could have those same n – 3 diagonals, but we'd be counting every single diagonal twice (one for each vertex), so we should divide that number by 2. We end up with the formula 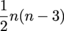 for the number of diagonals in an n-gon.
for the number of diagonals in an n-gon.
Sample Problem
How many degrees are in an octagon? How many non-intersecting and intersecting diagonals can we have?
Octagons have 8 sides, so n = 8. Now, all we need to do is apply our formulas (and remember what each of them stands for). Let's start with the number of degrees.
(n – 2) × 180° =
(8 – 2) × 180° =
6 × 180° =
1080°
Now for the number of non-intersecting and intersecting diagonals. We just gotta remember which formula is which.
n – 3 =
8 – 3 =
5
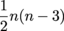 =
=
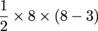 =
=
4 × 5 =
20
Not that difficult, considering there should always be fewer non-intersecting diagonals than intersecting ones. So basically, an octagon has a total of 1080° worth of interior angles, 5 non-intersecting diagonals, and 20 total diagonals.
One last tip: don't eat yellow snow.
Okay, for real. One last tip: if you find yourself dealing with a chunky polygon with far more sides than you can handle, try splitting it up into ones that you can handle. Basically, if you can break the polygon up into triangles and quadrilaterals, trust Nike and just do it. Seriously, though. it'll make your life way easier.
Example 1
How many distinct triangles can a dodecagon be divided into? |
Example 2
What is the total measure of the interior angles of a dodecagon? If the dodecagon is regular, what is the measure of one of these interior angles? |
Example 3
What's the perimeter of this pentagon?
|
Example 4
ΔABD is a right triangle, and EC || AB. What is the measure of ∠1?
|
Exercise 1
How many total diagonals does an undecagon have?
Exercise 2
How many distinct triangles can a 44-sided polygon be divided into?
Exercise 3
What is the sum of the internal angles of this polygon?

Exercise 4
What would be the measure of a single interior angle in a regular 15-gon?
Exercise 5
Which polygons are regular?

Exercise 6
What is the perimeter of the polygon shown?


