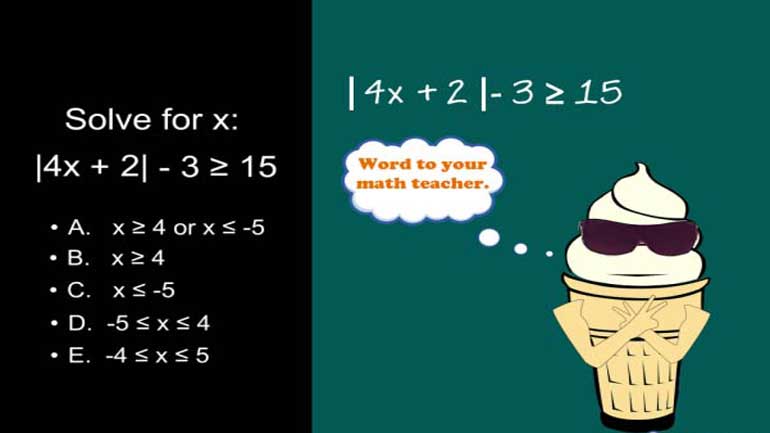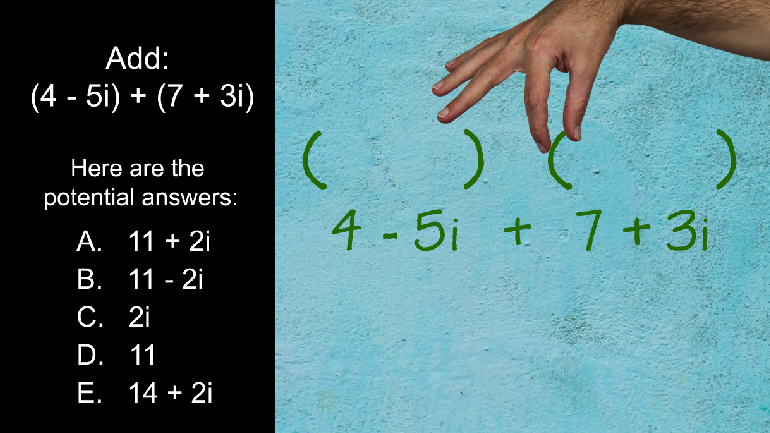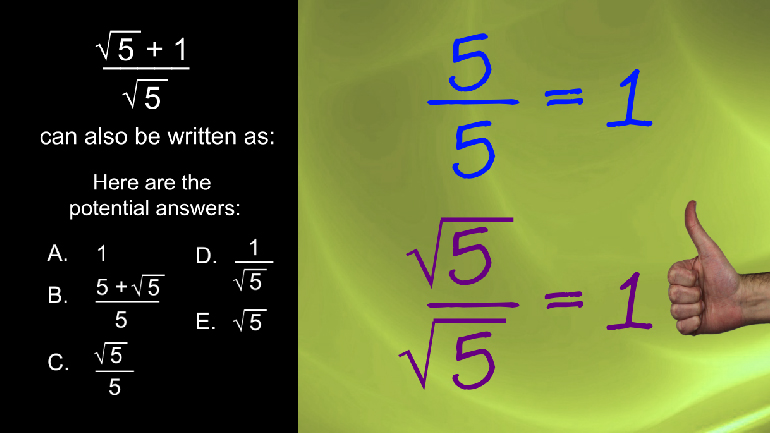ShmoopTube
Where Monty Python meets your 10th grade teacher.
Search Thousands of Shmoop Videos
Intermediate Algebra Videos 24 videos
ACT Math Intermediate Algebra Drill 2, Problem 5. Solve for x in this inequality.
ACT Math Intermediate Algebra Drill 1, Problem 3. Can you find the value of a in this expression?
ACT Math Intermediate Algebra Drill 1, Problem 5. Can you simplify the expression?
ACT Math 4.4 Intermediate Algebra 351 Views
Share It!
Description:
ACT Math: Intermediate Algebra Drill 4, Problem 4. Add these together.
- Intermediate Algebra / Complex numbers
- Product Type / ACT Math
- Foreign Language / Spanish Subtitled
- Foreign Language / Arabic Subtitled
- Foreign Language / Korean Subtitled
- Foreign Language / Chinese Subtitled
- Number and Quantity / Perform arithmetic operations with complex numbers
- Number and Quantity / Use complex numbers in polynomial identities and equations
- Number and Quantity / Perform arithmetic operations with complex numbers
- Number and Quantity / Use complex numbers in polynomial identities and equations
- Intermediate Algebra / Complex numbers
Transcript
- 00:02
Time for your daily dose of shmoop...this won't hurt a bit.
- 00:06
Add: quantity 4 minus 5i plus quantity 7 plus 3i.
- 00:11
And here are the potential answers...
- 00:15
OK, well this is actually a pretty simple question...
- 00:17
...the parentheses are thrown in here just to confuse you.
Full Transcript
- 00:20
So... uh... we can give them the old heave-ho.
- 00:23
Now we have 4 minus 5i plus 7 plus 3i...
- 00:26
...which is 11 minus 2i.
- 00:28
There we go. So boom! The answer is B.
Related Videos
ACT Math: Plane Geometry Drill 3, Problem 1. What is the area of the trapezoid shape in the video?
ACT Math: Coordinate Geometry Drill 1, Problem 1. Which inequality is expressed by the number line?
ACT Math: Intermediate Algebra: Drill 3, Problem 1. Find the fifth number in the series.
We don't like knocking people down to size, but we do like simplifying radicals. Join us?
If fleeing criminals always fled the scene of the crime at perfect right angles, it would be much easier to determine their whereabouts. Fortunatel...