ShmoopTube
Where Monty Python meets your 10th grade teacher.
Search Thousands of Shmoop Videos
Physics Videos 34 videos
Isaac Newton. Who was he? Why do we need to know about him? In a physics course, no less? Well, he's only the most famous physicist in history, and...
What are the basics of trigonometry? And why are we learning about this in a physics course? Both good questions. In this video, you'll learn about...
It's time to make our liters and meters work together. Enough of the bickering, right? In this video, we'll do some unit analysis, covering SI Unit...
Physics: Circular Motion 63 Views
Share It!
Description:
In this video, we'll cover inertia, centripetal force, circular motion, and what Newton liked to eat for breakfast in the morning (Apple Jacks).
Transcript
- 00:03
circular motion round and round around we go where we stop
- 00:06
well physics probably knows....
- 00:30
Well when you do crazy things [Man flying a plane]
- 00:36
at an airplane it's good to have a decent understanding of physics like
- 00:39
when you're flying upside down it's helpful to understand what you need to
Full Transcript
- 00:43
do to counteract the acceleration of gravity otherwise landing the plane [Plane landing upside down]
- 00:47
could come a bit you know earlier than you were hoping for a bit rougher - same
- 00:53
thing if you're gonna pull off a perfect loop-de-loop well you've got to know
- 00:57
what's creating your centripetal force so you know how to make it work in your
- 01:02
favor because no one likes a loop-de-loop that turns out to be a [Plane crashes into the floor]
- 01:07
know loop-de-crash especially the pilot so how does circular motion really work
- 01:12
well the key thing is centripetal force that's the force that's able to overcome
- 01:16
an object's inertia and create the circular motion well it turns out [Plane travels in a circular motion]
- 01:21
there's a handy little equation for centripetal force and it's this one
- 01:25
right here this equation says that centripetal force F sub C equals mass
- 01:31
times the square of the object's velocity divided by the radius of the
- 01:37
circle got it okay and this works for whatever the centripetal force is
- 01:41
whether that's tension, gravity or you know whatever and which comes in handy
- 01:46
when we know the equation for whatever type of centripetal force we're dealing [Equations for types of centripetal force]
- 01:50
with if the centripetal force is a friction
- 01:54
force for example we know that the equation for friction is the coefficient
- 01:57
of friction times the normal force so we have two equations for the same force we
- 02:03
set them equal to each other and use them to find values for unknown
- 02:07
variables now one of the basic laws of physics is that force equals mass [Formula for force]
- 02:12
times acceleration well Isaac Newton dropped his three laws of motion way [Isaac Newton underneath a tree]
- 02:16
back in 1687 and this equation was the basis of law number two because of this
- 02:23
law we can say that centripetal acceleration equals velocity squared
- 02:28
over the radius why well because everything is contained in the force
- 02:33
equation except the mass and there is always acceleration when it comes to [Moon orbiting the Earth]
- 02:38
circular motion even when the velocity is constant
- 02:42
remember velocity is the rate of displacement over time and it's a vector
- 02:48
quantity so it has both a magnitude and a direction acceleration is the rate of
- 02:52
change in velocity over time and in circular motion even if the magnitude of
- 02:57
velocity stays the same, the direction is constantly changing which means there's
- 03:03
constant acceleration even when the speed stays the same it's kind of like a
- 03:08
trick question of nature....
- 03:11
yeah circular motion can definitely make your head spin [Mans heading spinning in circular motion]
- 03:14
Now all this time we've been talking about centripetal
- 03:18
force like it's just one thing but there can be more than one force creating the
- 03:23
total centripetal force say we're planning with one of these cool toy [Man holding toy airplane]
- 03:27
airplanes well we tie some string around it and
- 03:30
spin it around vertically and wee boy! this is fun who needs an Xbox but let's
- 03:35
freeze it here at the top all right at this point what is the centripetal force [Airplane frozen at the top of the circular motion]
- 03:40
well we've definitely got tension on the string otherwise the toy plane here
- 03:44
would just keep going parallel to the ground so the tension on the string is
- 03:49
pointing to the center of the circle like any centripetal force does but
- 03:53
there's another force pointing that way too that would be our old pal gravity so
- 03:58
gravity and tension are working together to create the centripetal force in fact [Gravity and tension merge together]
- 04:02
we could even write this as an equation like this one - gravity plus tension
- 04:07
equals mass times velocity squared over the radius it's the opposite situation
- 04:12
when the plane is at the bottom of the circle here tension is pulling up toward [Arrow showing tension pulling upwards]
- 04:18
the center of the circle but gravity is still pointing down which means it's
- 04:23
pointing away from the center it's like a bad relationship you know
- 04:27
one minute they're working together the next they're in complete opposition and [A man and woman cuddling]
- 04:30
it just keeps going in circles and so at the bottom of the journey the equation
- 04:34
for centripetal force looks like this tension - gravity equals that
- 04:40
centripetal force equation which means that the tension in the string is having [Man holding a string]
- 04:44
to do a lot more work at the bottom of the circle than it is at the to
- 04:48
Now that we have some equations to work with we can start doing some actual
- 04:51
math... well back when I was just a little co-pilot my favorite thing at [Young boy wearing pilot gear at playground]
- 04:57
the playground was the merry-go-round you'd get that thing spinning so fast it
- 05:02
felt almost like flying... so let's say I put my son on one of these
- 05:06
contraptions he loves it the kiddo has a mass of 10 kilograms and [Son stood on a merry-go-round]
- 05:11
I get this thing spinning at a velocity of 5 meters per second it's pretty fast
- 05:16
if the radius of the merry-go-round is 5 meters
- 05:20
What's the kid's centripetal force and the centripetal acceleration....
- 05:25
well let's start with the centripetal acceleration since that's a component of
- 05:29
centripetal force like we've got to get that number first well the equation for
- 05:33
this acceleration is velocity squared over the radius and with a velocity of 5
- 05:38
meters a second and a radius of 5 meters we come up with an acceleration of 5 [Formula for son's centripetal force]
- 05:43
meters per second squared to find the amount of force we can just multiply the
- 05:47
acceleration by the mass which was 10 kilograms making the force 50 Newtons
- 05:52
hope the little tyke holds on tight there well flying yeah is in his blood [Boy falls off the merry-go-round]
- 05:57
Well after I convinced Jr. to basically never tell his mom about this
- 06:03
we'll head off to get some ice cream yeah...The landscape around here is a
- 06:06
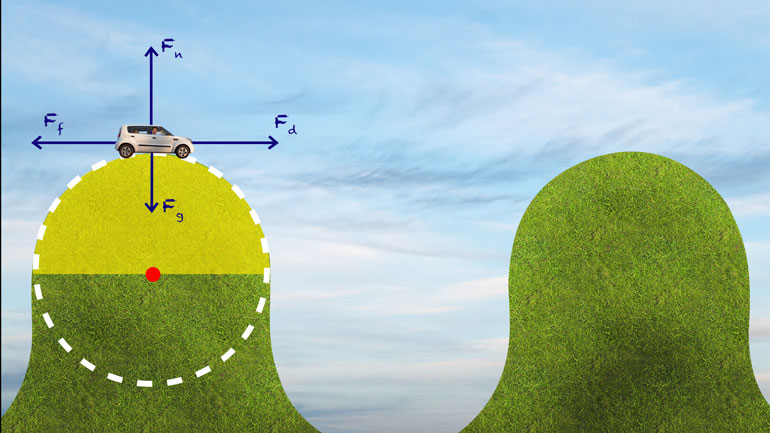
little weird lots of hills and valleys in there almost like half circles well [Car on top of a hill]
- 06:11
let's draw a force diagram for the car at the top of the hill and the bottom of
- 06:14
the valley all right then we can figure out what our centripetal force equations
- 06:18
would look like okay here we go so let's start at the top so we're in a moving
- 06:23
car which means we have the applied force from the engine pushing us forward
- 06:26
and friction is pushing in the other direction and how about along the y axis
- 06:30
well there's definitely gravity in the normal force to deal with but are they
- 06:35
equal or is one bigger than the other this is circular motion here people so [Circular motion appears at the top of the hill]
- 06:41
there has to be a centripetal force the center of the circle is straight down
- 06:45
and guess which direction gravity works yeah, that's our centripetal force
- 06:50
but we've also got the normal force of the road pushing up because we're
- 06:55
continuing in our circular motion there has to be acceleration right and in
- 06:59
order for there to be acceleration well we have to have a net force. If the
- 07:03
forces were equal in the net force was zero our motion would continue in the [Car flys across the hills]
- 07:07
direction of the velocity vector and we'd be catching air on this hill with
- 07:12
the tyke in his car seat back there I figure I should take it easy [Man in the car with his son in the backseat]
- 07:16
you know the straps aren't that tight...So gravity has to be stronger than the
- 07:20
normal force here we'll show that on our diagram by making the gravity arrow
- 07:24
longer than the one for normal force - now when we're at the bottom of the hill in [Car travels to the bottom of the hill]
- 07:29
the valley here the situation's reversed we've still got our applied force and
- 07:32
our friction but now the center of the circle is straight up just like the
- 07:36
normal force and the normal force has to be greater than gravity so it'll get the
- 07:41
longer arrow this time well you might have experienced this exact same thing [People riding a rollercoaster]
- 07:45
on a roller coaster think of going down that first big hill well at the bottom
- 07:50
you're pressed hard down into the seat that's because your inertia and gravity [Arrows point to inertia and gravity of people on a rollercoaster]
- 07:54
are working in similar directions your body wants to keep going in the same
- 07:58
downward angle of the hill and gravity is pushing you straight toward the
- 08:02
ground so as you're being pushed down harder into your seat your seats pushing
- 08:07
back up onto you with equal force so now all we have to do is figure out the [Car travels up the hill]
- 08:13
equations for centripetal force at each point in our ice cream trip... At
- 08:19
the top gravity minus normal force equals centripetal force and at the
- 08:23
bottom it's normal force minus gravity and at the ice cream shop it's vanilla [Man in the car at the ice cream store]
- 08:28
plus brownie fudge equals young yeah now sometimes Jr. gets bored so I
- 08:33
brought along that plane on a string that I was playing with earlier well [Man gives Jr a toy plane]
- 08:36
hopefully that'll keep him distracted long enough for me to finish the rest of
- 08:39
his frosty treat as he's swinging the plane around vertically let's do [Jr swining plane in garden]
- 08:43
something different at the top of the circle the plane has a velocity of 3
- 08:46
meters a second it has a mass of 0.5 kilograms and the force of tension on
- 08:51
the string is 15 Newtons let's put those numbers into a centripetal force
- 08:55
equation and use that to find the radius of the circle hmm well this is gonna be
- 09:00
a little trickier than what we've had to do before but it's nothing we can't
- 09:03
handle we have the toys mass and its velocity and we know the tension force
- 09:07
but we can't just plug all that into the centripetal force equation and solve for
- 09:12
R because tension isn't the only force that's in play here. At the top [Jr holding toy plane on a string and gravity line appears]
- 09:17
of the circle we've got gravity to factor in too - so our centripetal force
- 09:21
equation will be gravity plus tension equals mass times velocity squared over
- 09:26
the radius well since F sub G equals mass times the
- 09:30
acceleration of gravity we can sub in those variables the equation gravity
- 09:35
probably hasn't changed in the last few minutes so it's still 9.8 meters per
- 09:38
second squared multiplying that by point five kilograms gives us a force of
- 09:43
gravity of 4.9 Newtons and now we can plug in the numbers and find the radius
- 09:47
well 15 Newtons plus 4.9 Newtons equals 0.5 kilograms times the square of 3 [Formula to find the radius on a board]
- 09:54
meters per second over R when we do that first bit of addition, well we get
- 09:59
19.9 Newtons and rearranging that equation to solve for R [Equation rearranged to solve for R]
- 10:03
we find that R equals 0.5 kilograms times the square of 3 meters per second
- 10:08
over 19.9 Newtons and Mr. calculator tells us that the radius then
- 10:12
equals 0.23 meters it's a pretty tight turn there but we've got to use the
- 10:18
right amount of significant figures so the radius is 0.2 meters not
- 10:22
very big but big enough to do damage and that's what happens when you lose your [Boy swining toy plane on a string]
- 10:27
centripetal force okay time to go it's important to recognize when there are
- 10:32
two forces in action that are combining to create centripetal force or when
- 10:37
they're in opposition with one creating the centripetal force and one acting
- 10:41
against it and real life isn't always just up or down there might be times
- 10:45
when we have to break a diagonal force vector into x and y-components but we [Blue ball travelling in circular motion]
- 10:51
have all the skills now to handle that and even if we crash and burn on a
- 10:54
physics problem well there are worse ways
- 10:57
to crash and burn.. [Man parachuting down to the ground]
Related Videos
When you're about to marry the love of your life, not many things could stop you. However, finding out that your future hubby is keeping his crazy...
Here at Shmoop, we work for kids, not just the bottom line. Founded by David Siminoff and his wife Ellen Siminoff, Shmoop was originally conceived...
ACT Math: Elementary Algebra Drill 4, Problem 5. What is the solution to the problem shown?
AP® English Literature and Composition Passage Drill 1, Problem 1. Which literary device is used in lines 31 to 37?
AP® English Literature and Composition Passage Drill 2, Problem 1. What claim does Bacon make that contradicts the maxim "Whatsoever is delig...