ShmoopTube
Where Monty Python meets your 10th grade teacher.
Search Thousands of Shmoop Videos
Scientific Notation Videos 4 videos
Ever wish you didn't have to write out all those zeros when you counted your mounds of money? Well, there's a solution for that: scientific notatio...
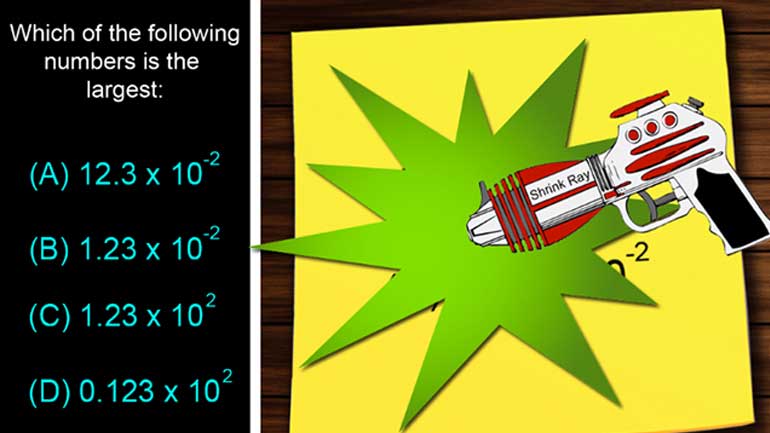
CAHSEE Number Sense: Drill Set 1, Problem 1. How would he write the number in scientific notation?
CAHSEE Math Number Sense: Drill Set 1, Problem 2. The decimal 0.000035 can be written in scientific notation as...what?
Scientific Notation 25560 Views
Share It!
Description:
Ever wish you didn't have to write out all those zeros when you counted your mounds of money? Well, there's a solution for that: scientific notation. It shortens those numbers down for your convenience.
Transcript
- 00:08
Scientific Notation, a la Shmoop. Congratulations! You just won a ton of money
- 00:17
in the lottery! Ay caramba. You're excited to tell the world
- 00:22
about your good fortune, but will that number even fit in a tweet?
- 00:29
Well, you'll need an easier way to express it. Thank goodness for Scientific Notation.
- 00:37
In short, Scientific Notation is a way of abbreviating numbers.
Full Transcript
- 00:43
Unlike names and words, you can't just trim out a few characters and expect it to mean
- 00:47
the same thing. It may sometimes seem like you have a ridiculous
- 00:50
amount of zeros, but each one is pretty important. You can't just remove them willy-nilly.
- 01:01
So we need the Scientific Notation to show how many zeros there are without actually
- 01:05
"showing" them. Here's how we do it...
- 01:11
Let's take that amount you won in the lottery... and simplify it.
- 01:16
First we have to grab all non-zero numbers -- in this case, "25."
- 01:22
Next, we have to convert this number to one that is greater than "1" but less than "10."
- 01:29
Send in the decimals. By plunking down a decimal in between the
- 01:34
2 and the 5, we get the number 2.5, which totally works
- 01:38
This number is referred to as our "coefficient." Our next job is to look at the number as a
- 01:45
whole... ...and count up the number of places to the
- 01:48
right of the decimal point.
- 01:53
Notice that we are not just counting up the zeros -- we also have to factor in the 5,
- 01:58
which is now also to the right of the decimal point
- 02:07
After some exhaustive counting, we see that there are 34 decimal places.
- 02:11
In Scientific Notation, we would write our complete number this way:
- 02:16
We've already established that "2.5" is our coefficient.
- 02:19
Because we are working in base 10, the "10" in our abbreviation is -- not surprisingly
- 02:23
-- called the "base." Finally, the 34 on the end that has been shrunken
- 02:28
down and raised up slightly is called..."the exponent."
- 02:35
And there you have it.
- 02:36
Remember, if given a number in Scientific Notation, you can always work backwards as
- 02:40
well. Or, you can just pay someone to do all the
- 02:42
work for you.
- 02:42
After all, you did just win two-point-five times ten to the thirty-fourth power dollars.
- 02:45
(GREAT NO CHANGES)
Related Videos
It's impressive that these expressions are able to stay so rational even when they're having operations performed on them.
Jack and Jill went up the hill to fetch a pail of water. But what happened when they got up there? They’ve been gone an awfully long time…
Sometimes, we just want fewer y's...or more x's. That's why it's great to know how to add and subtract variables. In real life, though, we try to a...