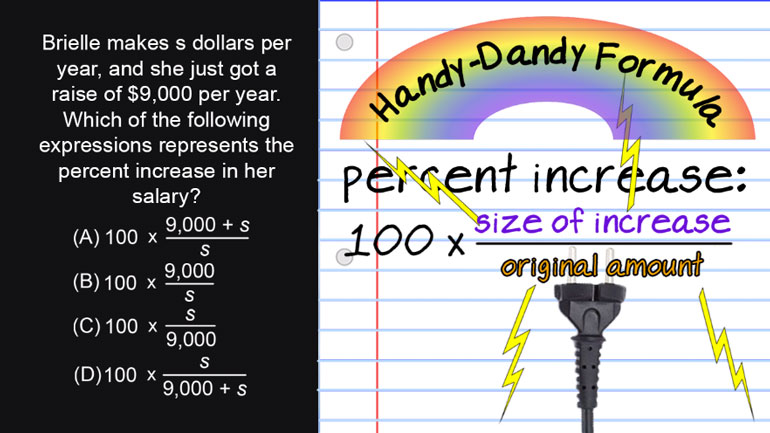
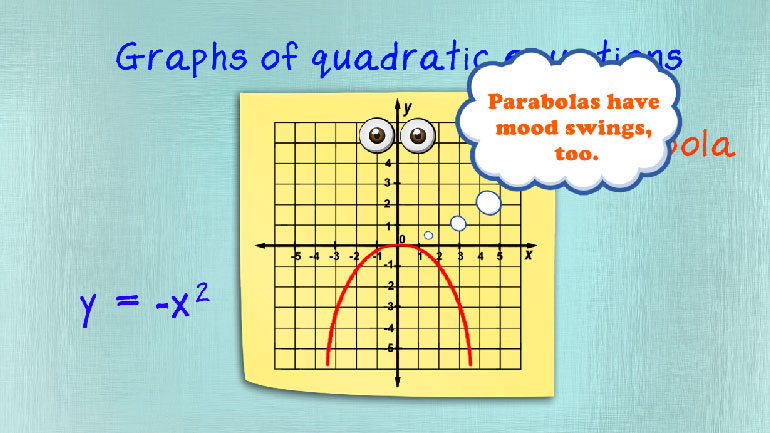
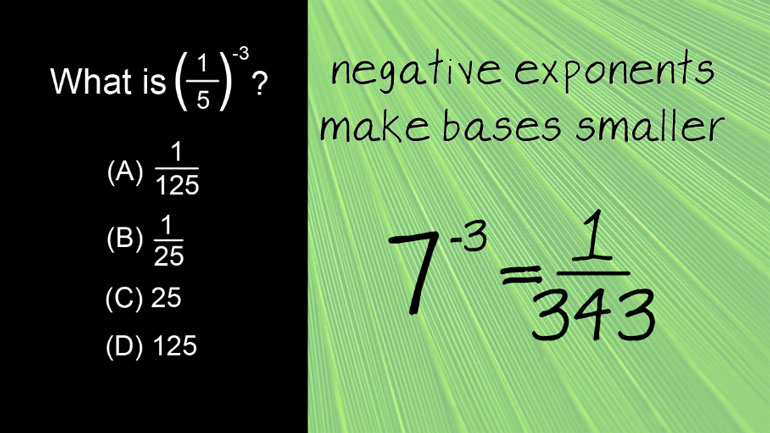ShmoopTube
Where Monty Python meets your 10th grade teacher.
Search Thousands of Shmoop Videos
Algebra II Videos 54 videos
Mosquitos need their caffeine, just like the rest of us. Wouldn't think zipping around and stinging people all day long sap your energy?
Tangent Half-Angle Formula 1363 Views
Share It!
Description:
Mosquitos need their caffeine, just like the rest of us. Wouldn't think zipping around and stinging people all day long sap your energy?
- Functions / Prove and apply trigonometric identities
- Functions / Prove and apply trigonometric identities
- Geometry / Understand and apply theorems about circles
- Circles / Understand and apply theorems about circles
- Trigonometry / Modeling using trigonometric functions
- Trigonometry / Use of trigonometric identities
Transcript
- 00:04
Tangent Half Angle Formula, a la Shmoop. Vido the Mosquito is exhausted after returning
- 00:12
from his business trip to Trigonometry Springs. Vido desperately needs an espresso. At Jolts
- 00:19
and Volts Coffee he orders his much needed jolt of caffeine.
- 00:23
As Vido digs in his pockets for theÉtangent of pi over eightÉ dollars he needs to pay
- 00:30
for his double shotÉ Éhe realizes he is in Half Angle-os and he
Full Transcript
- 00:34
only has Trig Springs money. In Half Angle-os, all money is converted using
- 00:44
the following formula: Tangent of u over 2 equals one minus the cosine
- 00:50
of u over sine of u. How will Vido convert his money to the correct
- 00:56
amount for his much needed coffee? First of all we can see that tangent of pi
- 01:01
over 8 can be rewritten as ? times pi over 4.
- 01:06
If we do this, we can get rid of the denominator 2 in our formula.
- 01:10
Then, if we substitute tangent of pi over 4 in for u, we get the following:
- 01:15
1 minus cosine of pi over 4 all divided by sine of pi over 4.
- 01:23
Since cosine of pi over 4 equals the square root of 2 over 2, and the sine of pi over
- 01:29
4 equals the square root of 2 over 2É Éour formula becomes:
- 01:33
1 minus the square root of 2 over 2 all over square root of 2 over 2.
- 01:40
Having too many terms just brings troubleÉ Éso first, to simplify the numerator, we
- 01:44
can put both terms under the same common denominator. Let's do this by multiplying 1 by 2 over 2,
- 01:50
to get 2 over 2 minus root 2 over 2. We subtract fractions by subtracting across
- 01:57
the numerator of the fractions and keeping the denominator the same, so we get 2 minus
- 02:03
root 2 over 2 on the top of the bigger fraction. We hate fractions in the denominator, so letÕs
- 02:12
multiply the numerator, 2 minus root 2 over 2É by the reciprocal of the denominator to
- 02:18
get rid of it. The 2 in the numerator and denominator cancel
- 02:23
out, so we're left with 2 minus root 2 divided by root 2.
- 02:27
We canÕt have radicals in the denominator, so we will rationalize it by multiplying the
- 02:32
fraction by root 2 over root 2. This gives us the fraction root 2 times the
- 02:38
quantity 2 minus root 2 all over 2. To simplify, letÕs distribute the root 2
- 02:45
across the quantity 2 minus root 2 to get 2 root 2 minus 2 all divided by 2.
- 02:52
Since we have a 2 on top and a 2 on bottom, they cancel each other out, so our final quantity
- 02:57
is root 2 minus 1. Fed up with having to go through so much math,
- 03:01
Vido throws his money at the barista and demands his coffee.
- 03:05
The barista calmly reaches back and points to a sign saying ÒWe reserve the right to
- 03:10
refuse service to anyone.Ó Maybe try the Starbugs across the street,
- 03:15
Vido.
Related Videos
This video can run circles around other videos about circles. Sir Cumference, of Round Table fame, explains all the properties of… well, circles....
Time to learn about the area of a sector. And no, that's not the sector's bedroom with a bumper sticker on the door that reads, "GO AWAY."
Equations of circles are a no-brainer. If aliens can do it, so can you. All you do is substitute the center of the circle's coordinates into the eq...
It's super useful to be able to find the distance around stuff. Like when you’re being pursued by authorities while running around the base of an...
ACT Math: Plane Geometry Drill 5, Problem 4. What is the radius and coordinate center of the circle?